Quantum Error Mitigation

from theory to practice

nate stemen
nate@unitary.foundation

Unitary Foundation

2025-02-07

Quantum Error Mitigation
from theory to practice

 
nate stemen

unitaryfund/mitiq

2025-02-07 @ QuSoft Seminar

Overview

  1. $ whoami
  2. Quantum Error Mitigation
  3. QEM Techniques
  4. QEM Feasibility
  5. import mitiq
  6. Unitary Foundation

$ whoami: nate stemen

What I Do:

  • Member of Technical Staff @ Unitary Foundation
  • Researcher & engineer in quantum error mitigation (QEM)
  • Maintainer of mitiq, an open-source QEM package
  • Interested in quantum software, and near-term use of QCs

Warning!

  • I am a practicioner.
  • I am not a theorist.

Why This Talk?

  • QEM is an attempt to bring quantum utility sooner

Quantum Error Mitigation (QEM)

Goal

Estimate \langle O \rangle = \mathrm{tr}(O \rho) given

  1. a quantum circuit C preparing \rho
  2. a noisy quantum device

Idea

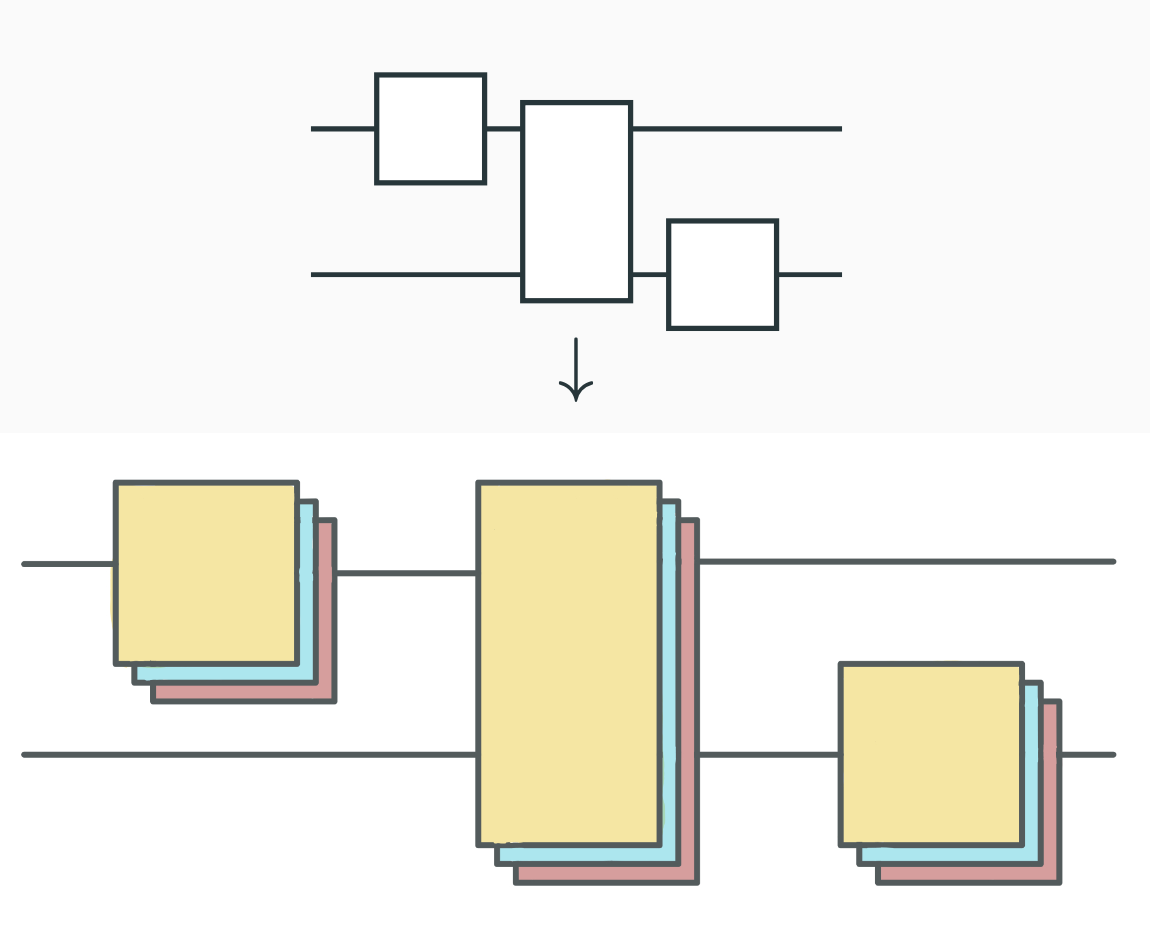
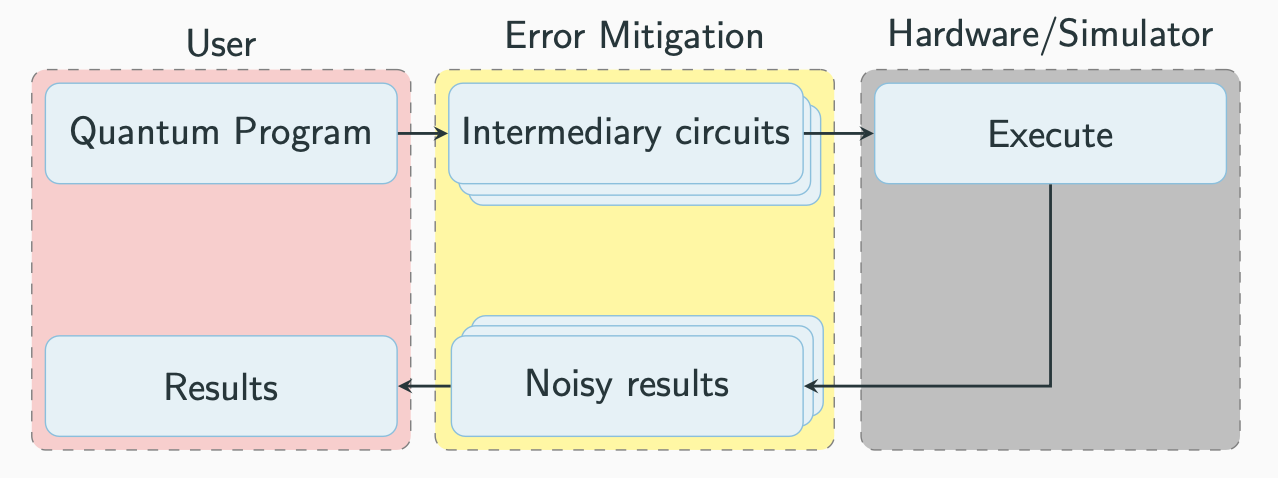
Algorithm is allowed to modify input circuit C and apply any postprocessing.

What about Error Correction?

Quantum Error Mitigation

  • Perform multiple different noisy computations
  • Collect results
  • Infer ideal expectation values

Quantum Error Correction

  • Encode logical qubits into many physical qubits
  • Mid-circuit measurements extract syndromes
  • Use syndromes to correct errors

Zero-Noise Extrapolation

\partial_t \rho = -i [H, \rho] + \textcolor{#F06292}{\lambda} \mathcal{L}(\rho)

  1. Run circuit of interest at higher noise levels C_{\textcolor{#F06292}{\lambda}}
  2. Measure \langle O \rangle_{\textcolor{#F06292}{\lambda}} = \mathrm{tr}(C_{\textcolor{#F06292}{\lambda}}|0\rangle\langle 0| O)
  3. Extrapolate and return \langle O\rangle_{\textcolor{#F06292}{0}}.

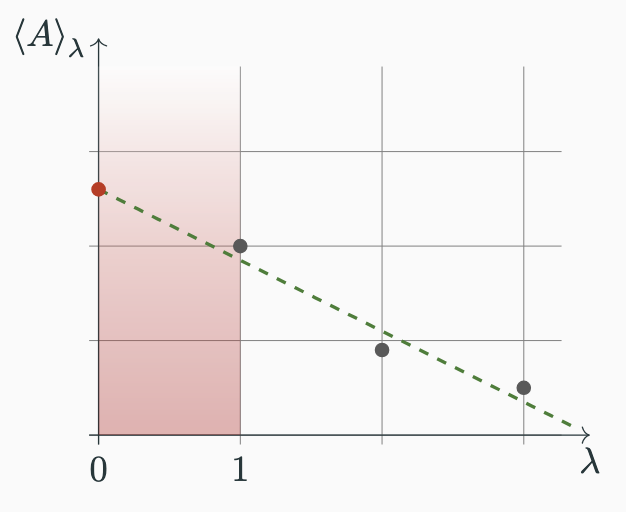
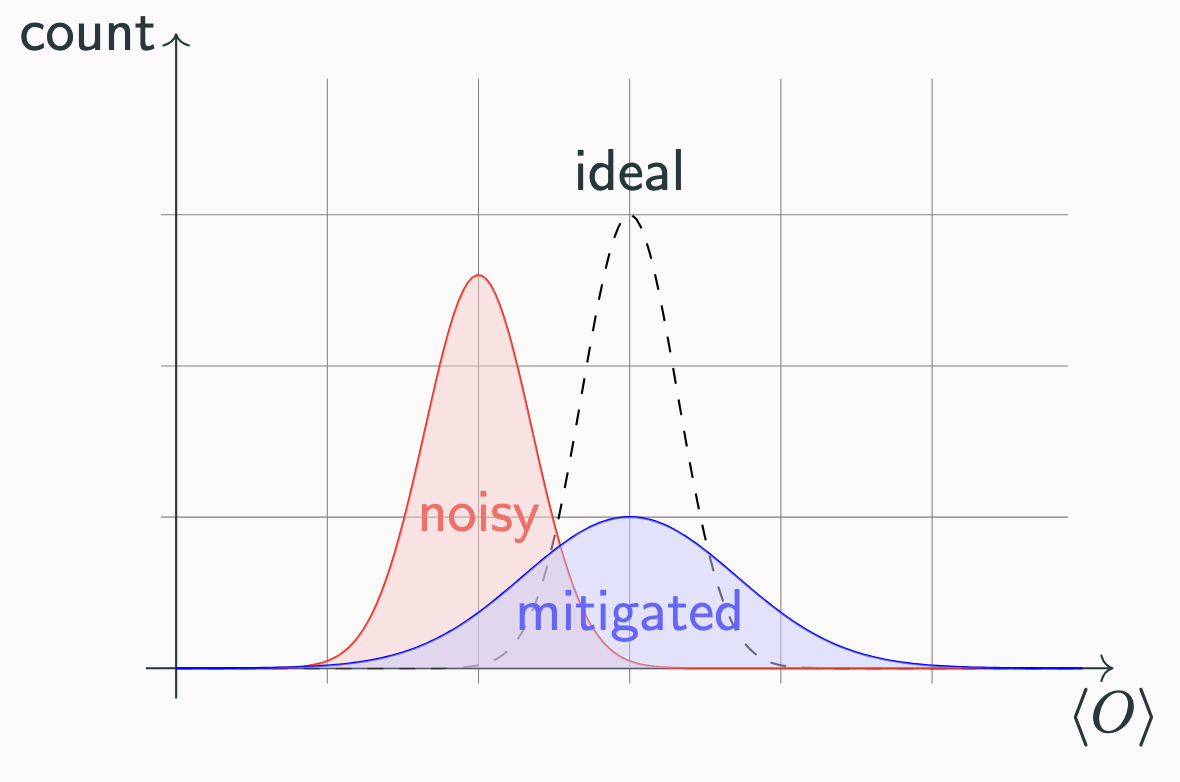
Key Idea

Scale noise up, extrapolate back to zero-noise value.

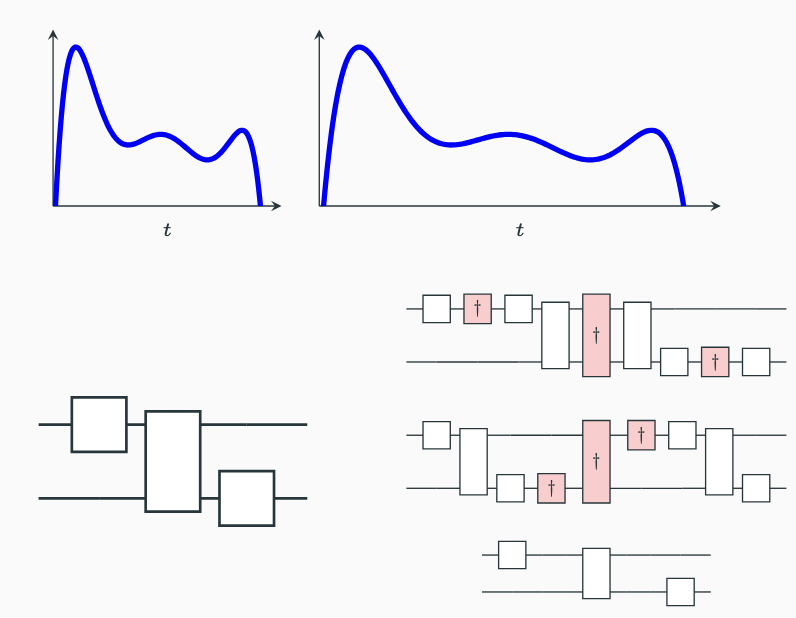
Probabilistic Error Cancellation

\mathcal{U}_\text{ideal} = \sum_{i=1}^n a_i \mathcal{O}_i

  1. Characterize implementable operations (basis gates)
  2. Construct representations of wanted gates
  3. Create circuits by sampling gates according to |a_i|
  4. Execute circuits
  5. Return \langle O\rangle_\text{PEC} = \frac{\gamma}{M}\sum_{i=1}^M \sigma_i \langle O \rangle_i

Key Idea

Use noisy operations to build ideal ones by selective cancellation and sampling.

QEM Feasibility

Feasibility Studies

Classical Noisy Simulation Algorithms

QEM Sample Complexity

Not Covered

Reducing the cost of QEC

Sampling Overhead

  • Suppose circuit contains G gates with error rate \varepsilon
  • \mathrm{Pr}[\text{no errors}] = (1 - \varepsilon)^G \approx \mathrm{e}^{-\varepsilon G}
  • Worst case lower bounded by \sim \mathrm{e}^{\varepsilon N L} (Takagi, Tajima, and Gu 2023)

Error mitigation is hopeless on circuits that scramble information rapidly. (Quek et al. 2024)

  • When \varepsilon NL = O(1), i.e. circuit size O(\varepsilon^{-1}) QEM is not prohibitive
Average 2Q Error \varepsilon Feasible circuit size
10^{-3} 100 \times 100
10^{-4} 300 \times 300
100 \times 1000
10^{-5} 1000 \times 1000
100 \times 10,000

(Zimborás et al. 2025)

QEM \bigcap QEC?

\varepsilon^{-1} = NL can be achieved in by QEC

Classical Noisy Simulation

A polynomial-time classical algorithm for noisy quantum circuits (Schuster et al. 2024)

any quantum circuit for which error mitigation is efficient on most input states, is also classically simulable on most input states

  • i.e. QEM efficient in the number of qubits
  • When \varepsilon = O(n^{-1}) circuit can be difficult to simulate and efficiently mitigable

Simulating quantum circuits with arbitrary local noise using Pauli Propagation (Angrisani et al. 2025)

  • Extending classical noisy simulation to more complex noise models
  • More complex qubit topologies

QEM Feasibility

import mitiq

Goal

Create a tool that anyone programming quantum computers can easily use.

requirements.txt

  • Easy to use
  • Minimal QEM knowledge
  • Works with QC access people already have
  • Works across SDKs

Docs!

mitiq.readthedocs.io

Recap

Feasibility

  • No outright refutation
  • Restrictions on QEM-feasible zone

Open Questions

  • Benchmarking QEM techniques
  • Average-case analysis for QEM sampling cost
  • Circuits for which QEM outperforms classical methods

In practice

  • Using error mitigation in practice is possible with mitiq
  • Tuning technique-parameters are often a challenge

Unitary Foundation

Software

Research

  • QEM
  • Benchmarking
  • Compilation

Ecosystem

  • Microgrant program
    • $4k; no strings attached
    • aimed at explorers in quantum
    • open-source, but also community projects
    • 3-6 month duration

Tip

Apply @ unitary.foundation/grants

Thank you!

Contact

📧 nate@unitary.foundation

References

Angrisani, Armando, Antonio A. Mele, Manuel S. Rudolph, M. Cerezo, and Zoë Holmes. 2025. “Simulating quantum circuits with arbitrary local noise using Pauli Propagation.” arXiv e-Prints, January, arXiv:2501.13101. https://doi.org/10.48550/arXiv.2501.13101.
Quek, Yihui, Daniel Stilck França, Sumeet Khatri, Johannes Jakob Meyer, and Jens Eisert. 2024. “Exponentially Tighter Bounds on Limitations of Quantum Error Mitigation.” Nature Physics 20 (10): 1648–58. https://doi.org/10.1038/s41567-024-02536-7.
Schuster, Thomas, Chao Yin, Xun Gao, and Norman Y. Yao. 2024. “A polynomial-time classical algorithm for noisy quantum circuits.” arXiv e-Prints, July, arXiv:2407.12768. https://doi.org/10.48550/arXiv.2407.12768.
Takagi, Ryuji, Hiroyasu Tajima, and Mile Gu. 2023. “Universal Sampling Lower Bounds for Quantum Error Mitigation.” Phys. Rev. Lett. 131 (November): 210602. https://doi.org/10.1103/PhysRevLett.131.210602.
Zimborás, Zoltán, Bálint Koczor, Zoë Holmes, Elsi-Mari Borrelli, András Gilyén, Hsin-Yuan Huang, Zhenyu Cai, et al. 2025. “Myths around quantum computation before full fault tolerance: What no-go theorems rule out and what they don’t.” arXiv e-Prints, January, arXiv:2501.05694. https://doi.org/10.48550/arXiv.2501.05694.